QUIN and Qualitatively Faithful Numerical Learning Last modified: March 2004, by Dorian Šuc

Dowload QUIN and Qfilter with a graphical user interface (for Windows, 13Mb); here is also a short users-guide to QUIN (it will be updated soon)

Homepage of Dorian Šuc

QUalitative INduction and Qualitative Trees

QUIN (QUalitative INduction) is a machine learning program that looks for qualitative patterns in numerical data. QUIN expresses such qualitative patterns by qualitative trees, that are similar to decision trees but have monotonicity constraints in leaves. Bellow is an example of a qualitative tree induced from a set of examples for the function Z=X²-X² (denoted by the red points on the right graph). The rightmost leaf, applying when attributes X and Y are positive, says that Z is strictly increasing in its dependence on X and strictly decreasing in its dependence on Y.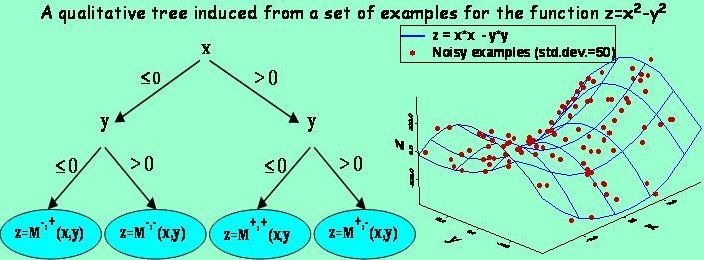

QUIN Applications and Qualitatively Faithful Numerical Learning

QUIN was applied in a number of domains, including reconstruction of human control strategies, qualitative reverse engineering of an industrial crane controller, qualitative system identification of a car wheel suspension system and others. Qualitative trees proved to provide a good insgiht into the modeled domain and enable (a possibly causal) explanation of relations among the variables.

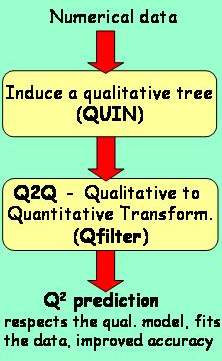Apart from explanation, the induced qualitative trees can be used to guide numerical regression. The resulting Q² (Qualitatively faithful Quantitative) predictions are guaranteed to be consistent with the induced qualitative model and are often considerably more accurate than those obtained by the state-of-the-art numerical learning methods (Q²was compared to LWR-Locally Weighted Regression, model and regression trees on datasets from UCI, Delve and others).

One method that enables such Q² prediction is Qfilter. It is based on quadratic programming and uses a qualitative tree and (not necessary) predictions of a base-learner (for example LWR, regression or model tree) to give numerical predictions that are consistent with the qualitative tree. When using the predictions of a base-learner, the differences (improvements) in numerical accuracy of the base-learner and Q² obviously come from the induced qualitative constraints.

Why Qualitative Consistency is Important?

Qualitative consistency of Q² predictions with a relatively simple and comprehensible (induced or provided) qualitative model enables that the numerical predictions are not obscured by qualitative inconsistencies that are usually very bothering for a domain expert. Such qualitative inconsistencies are quite usual even in simple learning problems.

Consider for example a container with a drain - the water leaks out and we are learning the time behaviour of water level given some measured time behaviors of water level. Of course, with all these learning examples water level always decreases in time. A usual numerical learner might predict that the water level in the container increases in time (despite the fact that the water is leaking and that the water level can never increase).

Some Related Publications (see also my other publications)

ŠUC, Dorian, Machine Reconstruction of Human Control Strategies, IOS PRess, Amsterdam, The Netherlands, 2003. Based on the dissertation awarded by the 2001 ECCAI Artificial Intelligence Dissertation Award.

ŠUC, Dorian, VLADUŠIČ, Daniel, BRATKO, Ivan. Qualitatively faithful quantitative prediction. Proceedings of the eighteenth International Joint Conference on Artificial Intelligence, pp. 1052-1057, San Francisco: Morgan Kaufmann Publishers, 2003. Acapulco, August, 2003.

ŠUC, Dorian, BRATKO, Ivan. Improving numerical prediction with qualitative constraints. Machine learning : ECML 2003 : proceedings, (Lecture notes in computer science, Lecture notes in artificial intelligence, vol. 2837), , pp. 385-396. Berlin; Heidelberg; New York: Springer, cop. 2003.

BRATKO, Ivan, ŠUC, Dorian. Learning qualitative models. AI Magazine. vol 24, no. 4, pp. 107-119, 2003.